1. Getting Started with Ergodic Insurance Framework

Welcome to the Ergodic Insurance Framework! This tutorial will help you get up and running with your first insurance optimization analysis in just a few minutes.

1.1. What You’ll Learn

By the end of this tutorial, you will:

• Install the framework and verify your setup

• Run your first manufacturer simulation

• Understand the basic output metrics

• Visualize wealth trajectories over time

• Learn where to go next

1.2. Prerequisites

• Python 3.12 or higher installed

• Basic familiarity with Python (ability to run scripts)

• No advanced mathematics or insurance knowledge required!

1.3. Installation

1.3.1. Step 1: Clone or Download the Framework

If you have git installed:

git clone https://github.com/AlexFiliakov/Ergodic-Insurance-Limits.git
cd Ergodic-Insurance-Limits

Or download the ZIP file from GitHub and extract it.

1.3.2. Step 2: Install Dependencies

We recommend using uv for faster installation:

pip install uv
uv sync

Alternatively, use standard pip:

cd ergodic_insurance
pip install -e .

1.3.3. Step 3: Verify Installation

Let’s verify everything is working:

# test_installation.py
from ergodic_insurance.manufacturer import WidgetManufacturer
from ergodic_insurance.claim_generator import ClaimGenerator
from ergodic_insurance.config_v2 import ManufacturerConfig

print("✅ Framework imported successfully!")

# Create configuration
config = ManufacturerConfig(
    initial_assets=10_000_000,
    asset_turnover_ratio=1.0,
    base_operating_margin=0.08,
    tax_rate=0.25,
    retention_ratio=0.7
)

# Create a simple manufacturer
company = WidgetManufacturer(config)

print(f"✅ Created company with ${company.assets:,.0f} in assets")
print("🎉 Installation successful!")

1.4. Your First Simulation

Now let’s run a real simulation to see how insurance affects your company’s growth trajectory.

1.4.1. Step 1: Create the Basic Setup

# first_simulation.py
import numpy as np
import matplotlib.pyplot as plt
from ergodic_insurance.manufacturer import WidgetManufacturer
from ergodic_insurance.claim_generator import ClaimGenerator
from ergodic_insurance.config_v2 import ManufacturerConfig

# Set random seed for reproducibility
np.random.seed(42)

# Configure the manufacturer
config = ManufacturerConfig(
    initial_assets=10_000_000,    # Starting with $10M
    asset_turnover_ratio=1.0,     # Generate revenue equal to assets
    base_operating_margin=0.12,        # Profit margin before losses (~8% margin after losses)
    tax_rate=0.25,                # 25% corporate tax
    retention_ratio=0.7           # Retain 70% of earnings
)

# Create a $10M widget manufacturer
manufacturer = WidgetManufacturer(config)

print(f"Company Profile:")
print(f"  Initial Assets: ${manufacturer.assets:,.0f}")
print(f"  Expected Annual Revenue: ${manufacturer.assets * config.asset_turnover_ratio:,.0f}")
print(f"  Expected Operating Income (Before Losses): ${manufacturer.assets * config.asset_turnover_ratio * config.base_operating_margin:,.0f}")

1.4.1.1. Expected Output:

Company Profile:
  Initial Assets: $10,000,000
  Expected Annual Revenue: $10,000,000
  Expected Operating Income (Before Losses): $1,200,000

1.4.2. Step 2: Set Up Loss and Premium Parameters

scenarios = 100
years = 20
deductible = 100_000

# Loss Parameters
regular_freq_baseline = 2.0
regular_sev_mean = 80_000
regular_sev_std = 50_000

cat_freq_baseline = 0.1
cat_sev_mean = 2_000_000
cat_sev_std = 1_500_000

# For regular losses (mean $80K), most will be below $100K deductible
# Calculate expected excess for lognormal distribution

# Lognormal parameters for regular losses
variance = regular_sev_std ** 2
mean = regular_sev_mean

sigma = np.sqrt(np.log(1 + variance / mean**2))
mu = np.log(mean) - sigma**2 / 2

# Generate sample to estimate excess over deductible
regular_sample = np.random.lognormal(mu, sigma, 100_000)
regular_excess = np.maximum(0, regular_sample - deductible)
regular_excess_pure_premium = regular_excess.mean() * regular_freq_baseline

# For catastrophic losses (mean $2M), nearly all will exceed $100K deductible
catastrophic_excess_pure_premium = (cat_sev_mean - deductible) * cat_freq_baseline

print(f"Baseline Revenue: {(config.initial_assets * config.asset_turnover_ratio):,.0f}")
print(f"Baseline Retained Losses: {(regular_sev_mean * regular_freq_baseline + cat_sev_mean * cat_freq_baseline - catastrophic_excess_pure_premium):,.0f}")

# Add expense loading
loss_ratio = 0.70
annual_premium_baseline = (regular_excess_pure_premium + catastrophic_excess_pure_premium) / loss_ratio

print(f"Baseline Annual Premium: {annual_premium_baseline:,.0f}")

1.4.2.1. Expected Output:

Baseline Revenue: 10,000,000
Baseline Retained Losses: 170,000
Baseline Annual Premium: 305,311

1.4.3. Step 3: Run the Simulation

bankruptcy_no_ins_scenarios = []
bankruptcy_with_ins_scenarios = []

scenarios_no_insurance = []
scenarios_with_insurance = []

for scen in range(scenarios):
    ### Configuration 1: No insurance #######
    all_scenario_claims_no_ins = []
    manufacturer_no_ins = WidgetManufacturer(config)
    wealth_no_insurance = [config.initial_assets]

    for year in range(years):
        revenue = manufacturer_no_ins.calculate_revenue()  # Current revenue
        revenue_scale = revenue / config.initial_assets

        # Regular losses: 4-6 per year on average, typically $50K-$150K
        regular_frequency = regular_freq_baseline * revenue_scale  # Scale with revenue
        regular_generator = ClaimGenerator(
            base_frequency=regular_frequency,
            severity_mean=regular_sev_mean,
            severity_std=regular_sev_std,
        )

        # Catastrophic losses: ~0.1 per year (once every 10 years), but can be $1M-$5M
        catastrophic_frequency = cat_freq_baseline * revenue_scale  # Also scales with revenue
        catastrophic_generator = ClaimGenerator(
            base_frequency=catastrophic_frequency,
            severity_mean=cat_sev_mean,
            severity_std=cat_sev_std,
        )

        # Generate regular losses for this year
        regular_claims, _ = regular_generator.generate_enhanced_claims(
            years=1,
            revenue=revenue,
            use_enhanced_distributions=False,
        )

        # Generate catastrophic losses for this year
        catastrophic_claims, _ = catastrophic_generator.generate_enhanced_claims(
            years=1,
            revenue=revenue,
            use_enhanced_distributions=False
        )

        # Combine all losses for this year
        year_claims = regular_claims + catastrophic_claims

        # For no insurance, company pays all losses over time without collateral
        for claim in year_claims:
            manufacturer_no_ins.process_uninsured_claim(claim.amount)

        manufacturer_no_ins.step()
        wealth_no_insurance.append(manufacturer_no_ins.assets)

    if manufacturer_no_ins.is_ruined:
        bankruptcy_no_ins_scenarios.append(scen)

    scenarios_no_insurance.append(wealth_no_insurance)

    ### Configuration 2: With insurance ($100K deductible, $200M limit) #######
    manufacturer_with_ins = WidgetManufacturer(config)
    wealth_with_insurance = [config.initial_assets]

    for year in range(years):
        revenue = manufacturer_with_ins.calculate_revenue()  # Current revenue
        revenue_scale = revenue / config.initial_assets

        # Regular losses: 4-6 per year on average, typically $50K-$150K
        regular_frequency = regular_freq_baseline * revenue_scale  # Scale with revenue
        regular_generator = ClaimGenerator(
            base_frequency=regular_frequency,
            severity_mean=regular_sev_mean,       # Mean claim size $80K
            severity_std=regular_sev_std,        # Moderate variation
        )

        # Catastrophic losses: ~0.1 per year (once every 10 years), but can be $1M-$5M
        catastrophic_frequency = cat_freq_baseline * revenue_scale  # Also scales with revenue
        catastrophic_generator = ClaimGenerator(
            base_frequency=catastrophic_frequency,
            severity_mean=cat_sev_mean,    # Mean catastrophic loss $2M
            severity_std=cat_sev_std,     # High variation - can reach $5M+
        )

        # Generate regular losses for this year
        regular_claims, _ = regular_generator.generate_enhanced_claims(
            years=1,
            revenue=revenue,
            use_enhanced_distributions=False,
        )

        # Generate catastrophic losses for this year
        catastrophic_claims, _ = catastrophic_generator.generate_enhanced_claims(
            years=1,
            revenue=revenue,
            use_enhanced_distributions=False
        )

        # Combine all losses for this year
        year_claims = regular_claims + catastrophic_claims

        # Process each claim through insurance
        for claim in year_claims:
            company_payment, insurance_payment = manufacturer_with_ins.process_insurance_claim(
                claim_amount=claim.amount,
                deductible_amount=100_000,
                insurance_limit=200_000_000
            )

        # Pay annual premium based on current revenue scale
        current_revenue = manufacturer_with_ins.calculate_revenue()
        revenue_scale = current_revenue / config.initial_assets
        annual_premium = annual_premium_baseline * revenue_scale
        manufacturer_with_ins.record_insurance_premium(annual_premium)

        manufacturer_with_ins.step()
        wealth_with_insurance.append(manufacturer_with_ins.assets)

    if manufacturer_with_ins.is_ruined:
        bankruptcy_with_ins_scenarios.append(scen)

    scenarios_with_insurance.append(wealth_with_insurance)

print(f"Bankruptcies (no insurance): {len(bankruptcy_no_ins_scenarios)}/{scenarios}")
print(f"Bankruptcies (with insurance): {len(bankruptcy_with_ins_scenarios)}/{scenarios}")

1.4.3.1. Sample Output:

<Several Insolvencies>
Bankruptcies (no insurance): 35/100
Bankruptcies (with insurance): 0/100

1.4.4. Step 4: Visualize the Results

# Create comprehensive visualization
fig = plt.figure(figsize=(15, 6))

### Plot 1: Wealth trajectories comparison #######
ax1 = plt.subplot()

bankrupt_no_ins = []
bankrupt_with_ins = []

# Plot all scenarios
for idx, s in enumerate(scenarios_no_insurance):
    if idx in bankruptcy_no_ins_scenarios:
        ax1.plot(range(len(s)), s, color='red', alpha=0.1)
        bankrupt_no_ins.append(s)
    else:
        ax1.plot(range(len(s)), s, color='orange', alpha=0.1)
for idx, s in enumerate(scenarios_with_insurance):
    if idx in bankruptcy_with_ins_scenarios:
        bankrupt_with_ins.append(s)
    ax1.plot(range(len(s)), s, color='blue', alpha=0.05)

# Compute and overlay means
no_ins_mean = np.average(np.array(scenarios_no_insurance, dtype=float), axis=0)
with_ins_mean = np.average(np.array(scenarios_with_insurance, dtype=float), axis=0)

ax1.plot(range(len(with_ins_mean)), with_ins_mean, color='blue', linewidth=2, alpha=0.8, label='With Insurance (mean)')
ax1.plot(range(len(no_ins_mean)), no_ins_mean, color='orange', linewidth=2, alpha=0.8, label='No Insurance (mean)')
ax1.axhline(y=100_000, color='r', linestyle='--', alpha=0.5, label='Bankruptcy')
ax1.axhline(y=config.initial_assets, color='gray', linestyle=':', alpha=0.5)

ax1.set_xlabel('Year')
ax1.set_ylabel('Wealth ($)')
ax1.set_title('Wealth Trajectories: Insurance vs No Insurance')
ax1.set_ylim(0, 20_000_000)
ax1.legend()
ax1.grid(True, alpha=0.15)

plt.tight_layout()
plt.show()

1.4.4.1. Sample Output:

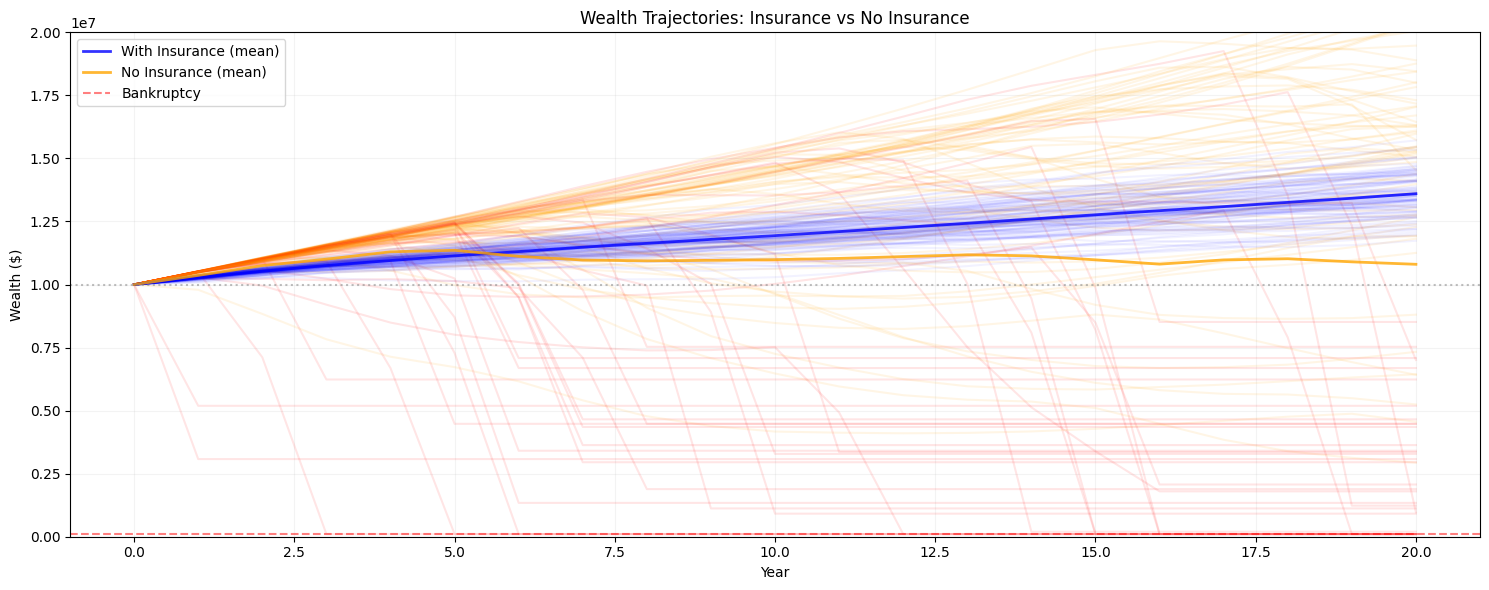
1.5. Understanding the Results

1.5.1. Why Insurance Creates Value

This demonstration shows the true value of insurance: protection against catastrophic losses that can bankrupt the company.

1.5.1.1. The Loss Structure

1. Regular Losses (~2 per year, $50K$150K each)

   • These are manageable without insurance

   • Total ~$160K per year on average

2. Catastrophic Losses (~0.1 per year, $1M-$5M each)

   • Occur roughly once every 10 years

   • Can exceed annual profits by 2-5x

   • These are what make insurance valuable

What’s not shown in this scenario is that catastrophic attritional losses (retaining too much below the deductible) can also matter, as can extremely large losses above the limit.

1.5.1.2. Key Insights

1. Not Buying Insurance Outperforms Insurance At First:

   • Ensemble Average dominates early on

   • As catastrophic losses get averaged into scenarios over time, the value of insurance emerges

2. The Catastrophic Protection:

   • Without insurance: A single loss can wipe out years of profits

   • With insurance: Maximum exposure is the deductible ($100K) per event

3. Long-term Growth Impact:

   • Insurance smooths the growth trajectory

   • Prevents bankruptcy during catastrophic years

   • Enables compound growth over time

1.5.2. What to Look For in the Graph

1. Wealth Trajectories (Top Left):

   • Light Red lines designate scenarios without insurance that go bankrupt

     • Notice that many of these outperform insurance early on

   • Light Red and Orange lines with steep drops designate catastrophic events

     • Notice how “No Insurance” drops sharply at these points

   • “With Insurance” shows smoother, more consistent growth

1.6. Common Patterns You’ll See in Future Simulations

1. The Insurance Paradox: Sometimes paying 2-3x expected losses in premiums is optimal!

2. Volatility Reduction: Insurance smooths the wealth trajectory

3. Growth vs. Safety Trade-off: Lower retention = safer but more expensive

4. Long-term Benefits: Insurance benefits compound over time

1.7. Next Steps

Now that you’ve run your first simulation, explore these topics:

1. Basic Simulation: Deep dive into the simulation mechanics

2. Configuring Insurance: Understanding layers, retentions, and limits

3. Optimization Workflow: Finding the optimal insurance strategy

4. Analyzing Results: Advanced metrics and decision-making

1.8. Quick Tips

• Start Simple: Begin with single-layer insurance before exploring complex programs

• Use Seeds: Set np.random.seed() for reproducible results during testing

• Experiment: Try different retention levels to see the trade-offs

• Think Long-term: Run simulations for 20-50 years to see ergodic effects

1.9. Getting Help

• Check the Troubleshooting Guide for common issues

• Review the FAQ for conceptual questions

• Explore the API Documentation for detailed function references

• Open an issue on GitHub

• Contact: Alex Filiakov

1.10. Summary

Congratulations! You’ve successfully:

• ✅ Installed the Ergodic Insurance Framework

• ✅ Created your first manufacturer model

• ✅ Generated realistic loss scenarios

• ✅ Run simulations with and without insurance

• ✅ Visualized and interpreted the results

You’re now ready to explore more advanced features and optimize your insurance strategy!